The traditional feed-forward neural networks are not good with time-series data and other sequences or sequential data. This data can be something as volatile as stock prices or a continuous video stream from an on-board camera of an autonomous car.
Handling time series data is where RNNs excel. They were designed to grasp the information contained in these sequences/time series data.
RNNs are built on the recursive formula, where the new state is a function of the old state and the input.
RNN applications extend beyond natural language processing and speech recognition. They’re used in language translation, stock predictions and algorithmic trading as well.
However, training RNNs come with their own set of challenges. For instance, the mathematical investigation of RNNs with respect to reliable information representation and generalization ability when dealing with complex data structures is still a challenge.
This has led to diverse approaches and architectures including specific training modes such as echo and liquid-state-machines, backpropagation decorrelation, or long short term memory, specific architectures such as recursive and graph networks, and hybrid systems.
Exploding And Vanishing Gradients
A gradient in the context of a neural network refers to the gradient of the loss function with respect to the weights of the network.
This gradient is calculated using backpropagation. The goal here is to find the optimal weight for each connection that would minimise the overall loss of the network.
While in principle the recurrent network is a simple and powerful model, in practice, it is, unfortunately, hard to train properly. The recurrent connections in the hidden layer allow information to persist from one input to another.
The exploding gradients problem refers to the large increase in the norm of the gradient during training. Such events are caused by the explosion of the long term components, which can grow exponentially more than short term ones.
The vanishing gradients problem refers to the opposite behaviour, when long term components go exponentially fast to norm 0, making it impossible for the model to learn the correlation between temporally distant events.
Why Bother About Gradients Vanishing At All?
Since the weights are updated proportional to the gradient, a vanishing gradient or a small value will result in a small change in the value of weight. The value of a weight, which is multiplied with the input, decides whether a certain input needs to be taken seriously or not. No change in value means the network isn’t learning anything. In short, there is no point in training.
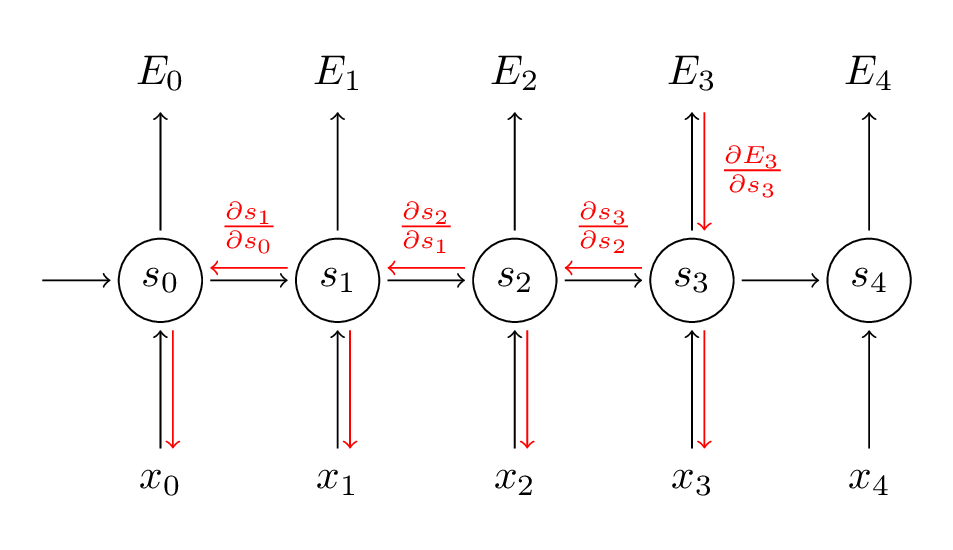
Let’s skim through the mathematical formulations that give an idea of why this problem occurs in the first place. The aim of a neural network is to reduce the losses/errors. As the errors are summed up, so are the gradients at each time step.
For one training example, the gradient can be written as:
See the full derivation here.
For intuition behind the above expression check the chain rule. The derivative of a vector function with respect to a vector is taken, the result is a matrix called the Jacobian matrix.
Jacobian may be regarded as a kind of “first-order derivative” of a vector-valued function of several variables. In particular, this means that the gradient of a scalar-valued function of several variables may too be regarded as its “first-order derivative”.
In other words, the Jacobian matrix of a scalar-valued function in several variables is (the transpose of) its gradient and the gradient of a scalar-valued function of a single variable is its derivative.
Activation functions don’t make things any better either. Since the sigmoid functions have derivatives of 0 at both ends, the corresponding neurons have a zero gradient and with small values in the matrix, the gradient values shrink exponentially fast, eventually vanishing completely after a few time steps.
Source: superdatascience
Depending on the activation function and hyperparameters, we could get exploding instead of vanishing gradients if the values of the Jacobian matrix are large.
Why Vanishing Gradients Are More Popular
- Exploding gradients are obvious. Gradients become NaN (not a number) eventually and whole training comes to a halt.
- The solution to exploding gradients are simple and effective such as having a pre-defined threshold
- The uncertainty of vanishing gradients makes them difficult to handle.
Vanishing gradients also appear in feedforward networks however, RNNs are more prone to them because of their nature of being recursive and deep layers.
Further reading sources:
https://arxiv.org/pdf/1211.5063.pdf





















































































