Reinforcement learning has been one of the most researched machine learning algorithms. As an algorithm that can be closely related to how human beings and animals learn to interact with the environment, reinforcement learning has always been given huge importance especially when it comes to branches of Artificial Intelligence such as robotics.
Reinforcement Learning is a reward based Machine Learning algorithm in which an agent learns to interact with its environment by performing an action that is either rewarded or penalized. The primary focus or objective of reinforcement learning is to help the agent maximize the cumulative reward with every action it performs.
In this article, we will learn about a Reinforcement Learning algorithm called Thompson Sampling, the basic intuition behind it and to implement it using Python. Thompson Sampling makes use of Probability Distribution and Bayes Theorem to generate success rate distributions.
What Is Thompson Sampling?
Thompson Sampling is an algorithm that follows exploration and exploitation to maximize the cumulative rewards obtained by performing an action. Thompson Sampling is also sometimes referred to as Posterior Sampling or Probability Matching.
An action is performed multiple times which is called exploration and based on the results obtained from the actions, either rewards or penalties, further actions are performed with the goal to maximize the reward which is called exploitation. In other words, new choices are explored to maximize rewards while exploiting the already explored choices.
One of the first and the best examples to explain the Thompson Sampling method was the Multi-Armed Bandit problem, about which we will learn in detail, later in this article.
Applications Of Thompson Sampling: Thompson Sampling algorithm has been around for a long time. It was first proposed in 1933 by William R. Thompson. Though the algorithm has been ignored and has had the least attention for many years after its proposal, it has recently gained traction in many areas of Artificial Intelligence. Some of the areas where it has been used are revenue management, marketing, web site optimisation, A/B testing, advertisement, recommendation system, gaming and more.
The Multi-Armed Bandit Problem
Though the name may sound creepy, Multi-Armed Bandit Problem (MABP), actually refers to multiple Slot machines. For those who are still confused, given below is the image of a single arm/lever slot machine.

Be glad if you haven’t ever seen one because as the name of the problem suggests these are bandits and their goal is to rob us. These machines are often popular in casinos where gamblers throw in a lot of money in the hope of winning big, most of them don’t.
Now let’s go back to the MABP. So the idea is all simple. Given multiple slot machines, like the one shown above, the goal is to maximize the reward for a person pulling the lever of each machine randomly.
If you were given five slot machines and a limited number of turns to pull the lever, how would you determine maximum success? Thompson Sampling is an approach that successfully tackles the problem.
Thompson Sampling makes use of Probability Distribution and Bayes Rule to predict the success rates of each Slot machine.
Basic Intuition Behind Thompson Sampling
- To begin with, all machines are assumed to have a uniform distribution of the probability of success, in this case getting a reward
- For each observation obtained from a Slot machine, based on the reward a new distribution is generated with probabilities of success for each slot machine
- Further observations are made based on these prior probabilities obtained on each round or observation which then updates the success distributions
- After sufficient observations, each slot machine will have a success distribution associated with it which can help the player in choosing the machines wisely to get the maximum rewards
Implementing Thompson Sampling With Python
Let us consider 5 bandits or slot machines. Initially, we do not have any data on how the probability of success is distributed among the machines. So we start by exploring the machines one by one.
Say after 200 observations we have data similar to what’s shown below:
Each column represents a bandit or a slot machine (B1, B2, B3, B4 and B5). The 0’s represent penalties or the player not getting a reward and all the 1’s represent the player winning a reward while pulling the arm of the slot machine.
We have 200 observations, which means that the player pulled the lever/arm of each machine 200 times.
Run the below code block to generate a similar dataset.
import random
import pandas as pd
data = {}
data['B1'] = [random.randint(0,1) for x in range(200)]
data['B2'] = [random.randint(0,1) for x in range(200)]
data['B3'] = [random.randint(0,1) for x in range(200)]
data['B4'] = [random.randint(0,1) for x in range(200)]
data['B5'] = [random.randint(0,1) for x in range(200)]
data = pd.DataFrame(data)
Let’s Implement Thompson Sampling!!
We will use one of the simplest implementations of Thompson sampling in Python.
Since we have to iterate through each observation of each of the 5 machines, we will start by initializing the number of observations and machines.
observations = 200
machines = 5
In Thompson Sampling each machine is selected based on the beta distribution of rewards and penalties associated with each machine. And so we need a list to save the machine that has been selected by Thompson Sampling for a specific round/observation.
machine_selected = []
We will now initialize 3 variables,
- one to store the rewards or 1’s received by each Slot Machine/Bandit that was selected by the Thompson Sampling algorithm,
- one to store the penalties or 0’s received by each Slot Machine/Bandit that was selected by the Thompson Sampling algorithm, and,
- a variable to store the total number of rewards obtained using the Thompson Sampling algorithm
rewards = [0] * machines
penalties = [0] * machines
total_reward = 0
Note:
Each of the above variables is initialized with zero as we do not know prior to the algorithm. Also, the first two variables are lists as it stores the values of each machine. In this case 5 machines.
Now let’s begin Thompson Sampling!
For each observation ‘n’ in the dataset, we start with the machine B1 and a default maximum beta distribution of zero.
for n in range(0, observations):
bandit = 0
beta_max = 0
Now for each observation, we will iterate through each machine and will select the machine with the highest random beta distribution.
for i in range(0, machines):
beta_d = random.betavariate(rewards[i] + 1, penalties[i] + 1)
if beta_d > beta_max:
beta_max = beta_d
bandit = i
Now update the list ‘machine_selected’ with the bandit/machine selected by the Thompson Sampling.
machine_selected.append(bandit)
Once we have selected the machine, we will check the dataset for that specific machine and the number of observation, if it returned a reward or penalty. If it is a reward, we will update the list ‘rewards’ by adding one to that specific machine/bandit, if it is a penalty we will update the list ‘penalties’ by adding one to that specific machine/bandit. We will then update the total reward.
reward = data.values[n, bandit]
if reward == 1:
rewards[bandit] = rewards[bandit] + 1
else:
penalties[bandit] = penalties[bandit] + 1
total_reward = total_reward + reward
Let’s visualize our results:
print("\n\nRewards By Machine = ", rewards)
print("\nTotal Rewards = ", total_reward)
print("\nMachine Selected At Each Round By Thompson Sampling : \n", machine_selected)
Output:
Rewards By Each Machine
#Visualizing the rewards of each machine
plt.bar(['B1','B2','B3','B4','B5'],rewards)
plt.title('MABP')
plt.xlabel('Bandits')
plt.ylabel('Rewards By Each Machine')
plt.show()
Output:
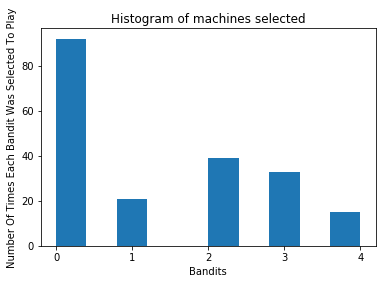
Number Of Times Each Machine Was Selected
#Number Of Times Each Machine Was Selected
from collections import Counter
print("\n\nNumber Of Times Each Machine Was Selected By The Thompson Sampling Algorithm : \n",dict(Counter(machine_selected)))
Output:
Number Of Times Each Machine Was Selected By The Thompson Sampling Algorithm :
{2: 39, 1: 21, 3: 33, 0: 92, 4: 15}
#Visualizing the Number Of Times Each Machine Was Selected
plt.hist(machine_selected)
plt.title('Histogram of machines selected')
plt.xlabel('Bandits')
plt.xticks(range(0, 5))
plt.ylabel('No. Of Times Each Bandit Was Selected')
plt.show()
Output:
By comparing the two graphs, we can see that Thomson Sampling wisely selected the machines which gave more rewards the most number of times.
Here is what the complete code with proper indentations would look like: