With the onslaught of neural networks and deep learning, the breadth of tasks carried out by a computer has grown very fast. Neural networks have managed to learn to represent and manipulate numerical data. But at the same time, it is hard for these kinds of machine algorithms to generalise the data from outside the training regime. The researchers at Google Deepmind, the University of Oxford and the University College London have come up with a way to teach computers to count. The researchers have come up with a neural arithmetic logic unit.
The research is some way follows the work done by Alex Graves who invented the Neural Turing Machine (NTM) which tries to bind values to specific locations by designing neural networks that has an external memory. There are major differences between the functioning of neural networks and our brain. The biggest difference is the memory. Ability to read and write from memory is critical and both the computer and the brain can do it, but not with Neural networks. Previously, Alex Graves and fellow researchers at DeepMind aimed to build a differentiable computer, which could put together a neural network and link it to external memory. The neural network would act like a CPU and with the memory attached, the aim would be to learn programs (algorithms) from input and output examples.
Previous Failures In Numerical Extrapolation
The researchers develop a new module that can be plugged into conventional architectures to learn numerical computations. The strategy is of the researchers is to represent numerical quantities with a single neuron. The researchers applied operators like simple functions such as +, −, ×, to these single neurons. Surprisingly these neurons are still differentiable and this makes it possible for us to learn them with backpropagation. The researchers work with various data and domains such as images, code and text and using supervised and reinforcement learning.
The researchers have also done a good work of showing how standard networks have failed in numerical extrapolation. To this end, they trained an autoencoder to take the scalar value as an input and encode it in the hidden layers and then reconstruct before the output layers. They observed that many architectures fail to represent numbers that the networks have not seen during the training. The researchers also observe that highly linear (such as PReLU) beat sharply nonlinear functions such as sigmoid and tanh. This is a strange behaviour since this is counter-intuitive. The researchers in an attempt to test this, trained around 100 models to encode numbers between −5 and 5 and tested their ability to encode numbers between −20 and 20.
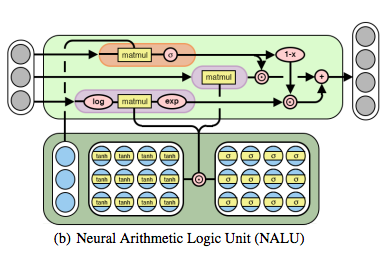
Neural Arithmetic Logic Unit
The researchers propose two models that are taught to manipulate numbers. The first model is called the neural accumulator (NAC), which researchers state that, “neural accumulator is a special case of a linear (affine) layer whose transformation matrix W consists just of −1’s, 0’s, and 1’s; that is, its outputs are additions or subtractions (rather than arbitrary rescalings) of rows in the input vector.” This ensures consistency throughout the model, and there is no dependency on the number of operations are chained together.
Since it is easy to learn, whose elements are [−1, 1] and biased to be close to −1, 0, or 1. The model does not have a bias vector, and no squashing nonlinearity is applied to the output. We would also like to have the powers of multiplication, division along with the simpler addition and subtraction operations.
The second model design is known as the neural arithmetic logic unit (NALU). This model learns a weighted sum between two subcells. Both of the cells have their own function where one cell has the property of doing simple operations like addition and subtraction and other is responsible for complex operations like multiplication, division, and power functions. NALU is related to the NAC. When we extend NAC with gate-controlled sub-operations we get a NALU.
Experiments And Results
The researchers put on many test cases to work on numeric reasoning and extrapolation of the above architectures. The researchers state that, “We study the explicit learning of simple arithmetic functions directly from the numerical input, and indirectly from image data. These supervised tasks are supplemented with a reinforcement learning task which implicitly involves counting to keep track of time.” The researchers try to have NALU learn some simple function learning tasks and they showcase the ability of NACs and NALUs. They show how these two architectures can learn to select relevant inputs and apply different arithmetic functions to them. Results show that NALU outperforms traditional neural architectures on many extrapolation tasks.
Apart from the counting tasks, they also tested the performance of the architecture in program evaluation. This task is a perfect test for this architecture because program evaluation requires as researchers state, “the control of several logical and arithmetic operations and internal book-keeping of intermediate values.” Researchers test consists of tasks like simply adding two large integers, and evaluating programs containing several operations (if statements, +, −). In this particular task also they found that only NALU architecture was able to extrapolate to larger numbers.
The researchers conclude by saying, “We have shown how the NAC and NALU can be applied to rectify these two shortcomings across a wide variety of domains, facilitating both numerical representations and functions on numerical representations that generalise outside of the range observed during training. This design strategy is enabled by the single-neuron number representation we propose, which allows arbitrary (differentiable) numerical functions to be added to the module and controlled via learned gates, as the NALU has exemplified between addition/subtraction and multiplication/division.”